
Популярные задачи:
Найти максимальную сумму в последовательности
- Вступление
- Задача и простой алгоритм
- Кубический алгоритм (N3 очень медленно!)
- Два квадратичных алгоритма (~N2)
- И второй квадратичный
- Алгоритм «разделяй и властвуй» (~N*LgN)
- And winner is... сканирующий (линейный) алгоритм!
- Подробней про замеры
- История
- Ценные методы, подходы
- Все реализации
Вступление
Одна из самых интересных задач. На ее примере познаются многие, очень полезные подходы для написания быстрых, хороших алгоритмов. К сожалению, данная задача в чистом виде, как выясняется - мало где применяется: а случаи отличные от одномерного - требуют написания алгоритмов намного сложней, и намного менее красивых чем приведенные здесь.
По книге Джона Бентли:
"Жемчужины программирования"
Задача и простой алгоритм
Задача эта появляется при распознавании одномерного шаблона; к ее истории мы обратимся позже. На входе имеется массив X из N вещественных чисел, на выходе должна быть получена максимальная сумма любой непрерывной последовательности элементов массива. Например, если во входном массиве содержатся следующие 10 элементов (рис. 8.1):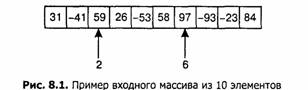
- программа должна вернуть сумму х[2..6], то есть 187. Задачу легко решить с положительными числами — максимальная сумма будет равна сумме всех элементов массива. Проблема возникает, когда появляются отрицательные числа: стоит ли включать такой элемент в выбранную последовательность, надеясь, что соседние компенсируют его? Чтобы завершить постановку задачи, скажем, что когда все элементы массива отрицательны, на выходе должна быть сумма элементов пустой последовательности элементов массива, равная нулю.
Кубический алгоритм (N3 очень медленно!)
Первый вариант программы, который приходит в голову, перебирает все пары целых i и j, где 0<=i<=j
Программа короткая, ясная, ее легко понять. К сожалению, она работает медленно. На моем компьютере(прим. ред: в те времена) ей требуется 22 минуты, если n=10 000, и 15 дней, если n=100 000. Вопросы, связанные с временем выполнения, будут детально рассмотрены ниже в разделе про замеры производительности.
Конкретные данные о времени работы программы хорошо приводить в байках, но почувствовать реальную эффективность алгоритма можно, используя оценку эффективности с помощью понятия «О-большое». Внешний цикл выполняется ровно n раз, средний — не более n раз на каждый из проходов внешнего цикла. Перемножив эти величины, получим, что код внутри среднего цикла выполняется О(n2) раз. Внутренний цикл выполняется не более n раз, поэтому его мы тоже записываем как О(n). Перемножив все эти величины, получим, что время работы алгоритма пропорционально n3. Такие алгоритмы называются кубическими.
Этот пример иллюстрирует метод анализа с помощью «О-большого», а также его сильные и слабые стороны. Главный недостаток его в том, что мы все равно не знаем, сколько будет работать программа при конкретных входных данных, а знаем лишь, что количество шагов будет О(n3). Этот недостаток обычно компенсируется двумя сильными сторонами метода: анализ с помощью «О-большого» легко производить (как в примере выше), а информация об асимптотическом поведении алгоритма обычно достаточна для предварительных оценок эффективности.
Далее по тексту асимптотическое время работы алгоритма используется в качестве единственной оценки производительности программы. Более высокая точность анализа для данной задачи разбирается ниже в разделе про замеры. Прежде чем читать дальше, задумайтесь на минуту и попробуйте найти более быстрый алгоритм.
Два квадратичных алгоритма (~N2)
Большинство программистов реагируют на алгоритм 1 одинаково: «есть очевидный способ сделать его намного быстрее». Таких способов на самом деле два, причем конкретному программисту обычно очевиден лишь один из двух. Оба алгоритма обладают квадратичным временем работы — делают О(n2) операций для массива размером n — и в обоих сумма x[i..j] вычисляется за постоянное количество шагов, а не за j-i+1 сложений, как в алгоритме 1. Однако эти два алгоритма используют принципиально различные методы вычисления сумм за конечное число шагов.
Первый квадратичный алгоритм позволяет быстро вычислить сумму благодаря тому, что сумма x[i..j] легко получается из предыдущей: x[i..j-l]. Использование этого свойства позволяет получить алгоритм:
Операторы внутри внешнего цикла выполняются n раз, а те, что лежат внутри внутреннего, — не более чем n раз, так что время работы алгоритма составляет О(n2).
И второй квадратичный
Альтернативный квадратичный алгоритм вычисляет сумму во внутреннем цикле, обращаясь к структуре данных, которая строится отдельно, до начала первого цикла. Создается массив cumarr, 1-й элемент которого содержит кумулятивную сумму значений х[0..i], поэтому сумму x[i...j] можно получить как разность cumarr[j] -cumarr[i-l]. В итоге получим:
Этот код требует также О(n2) операций; анализ проводится так же, как и для квадратичного алгоритма №1.
Рассмотренные три варианта алгоритмов исследуют все возможные пары начального и конечного индексов, вычисляя сумму элементов последовательности. Поскольку таких последовательностей О(n2), ни один алгоритм, проверяющий их все, не может быть быстрее квадратичного. Можете ли вы придумать способ обойти проблему и получить более быстрый алгоритм?
Алгоритм «разделяй и властвуй» (~N*LgN)
Первый из быстрых алгоритмов, по времени выполнения он линейно-алгорифмичный и при этом достаточно сложен, поэтому если вы запутаетесь в деталях, можете перейти сразу к следующему разделу, вы не слишком много потеряете при этом. Итак, алгоритм основан на следующем правиле:
!Если нужно решить задачу размера n, следует рекурсивно решить 2 подзадачи размера приблизительно n/2, а затем объединить их решение в единое целое!
В данном случае мы имеем дело с массивом размера n, поэтому наиболее естественным способом разделения задачи на 2 подзадачи будет создание 2-х массивов приблизительно одинаковогоразмера. Один из ним мы назовем A, а другой B:
| A | B |
Затем мы рекурсивно найдем подпоследовательности с максимальной суммой элементов в масивах A и B; одну из них назовем ma, а другую - mb:
| ma | mb |
Соблазнительная мысль о том, что мы решили задачу, потому что подпоследовательность всего массива с максимальной суммой должна равняться либо ma, либо mb, оказывается неправильной, потому что эта искомая подпоследовательность может и пересекать границу между A и B. Такую подпоследовательность мы назовем mc, поскольку она пересекает границу.
| mc |
Итак, наш алгоритм "разделяй и властвуй" должен рекурсивно находить ma и mb, после чего каким-то другим способом находить mc и сравнивать их между собой.
Этого описания почти достаточно для написания программы. Осталось лишь определить способ работы с массивами малого размера и способ вычисления mc. Первое сделать несложно: подпоследовательность с максимальной суммой для массива из одного элемента равна этому элементу, если он положителен, или нулю, если элемент отрицателен, а максимальная подпоследовательность пустого массива равна нулю. Для вычисления mc отметим, что его левая часть представляет собой максимальную подпоследовательность элементов, заканчивающуюся на границе A и B и простирающуюся в A, а правая часть - такую же подпоследовательность, лежащую в B. Собрав все это вместе, получим следующий алгоритм:
Код достаточно сложен, в нем легко ошибиться, но он решает задачу за О(n log n) операций. Мы можем доказать это несколькими способами. Неформальное доказательство заключается в том, что алгоритм выполняет работу О(n) на каждом из O(log n) уровней рекурсии. Доказательство можно сделать более строгим, используя рекуррентные соотношения. Если Т(n) обозначает время решения задачи размера n, то Т(1) = О(1) и Т(n) = 2Т(n/2) + О(n).
And winner is... сканирующий (линейный) алгоритм!
Воспользуемся простейшим алгоритмом для работы с массивами. Начинать следует с левого конца массива (элемента х[0]), затем нужно перебрать все элементы и закончить на правом конце (элемент х[n-1]), все время сохраняя информацию о наилучшей на данный момент сумме. Изначально максимальная сумма равна нулю. Предположим, что мы решили задачу для х[0. .i-1], как можно расширить ее решение, добавив в него элемент x[i]? Используем те же соображения, что и для алгоритма «разделяй и властвуй»: подпоследовательность первых i элементов с максимальной суммой может либо целиком лежать в первых i элементах (хранится в maxsofar), либо заканчиваться элементом i (хранится в maxendinghere):
| maxsofar | maxendinghere |
Вычисление maxendinghere каждый раз заново, аналогично алгоритму 3, даст нам в итоге еще один квадратичный алгоритм. Мы можем обойти это, используя тот же метод, который привел нас к алгоритму 2: вместо того, чтобы находить максимальную подпоследовательность, заканчивающуюся элементом i, мы воспользуемся максимальной подпоследовательностью, заканчивавшейся элементом i-1. В итоге получаем алгоритм 4:
Ключ к пониманию этой программы — переменная maxendinghere. Перед первым оператором присваивания в цикле значение переменной равно максимальной сумме подпоследовательностей, заканчивающихся элементом i-1. Оператор присваивания изменяет ее содержимое таким образом, что оно становится равным максимальной сумме подпоследовательностей, заканчивающихся элементом i. Оператор увеличивает это значение добавлением x[i] до тех пор, пока это действие оставляет сумму подпоследовательности положительной; возможные отрицательные значения заменяются нулем, поскольку максимальная по сумме подпоследовательность, заканчивающаяся элементом i, теперь является пустой. Хотя этот код труден для понимания, он прост и быстр, потому что выполняется за О(n) операций. Такие алгоритмы называются линейными.
Подробней про замеры
Пока что мы действовали довольно безответственно, используя «О-большое». Пришло время поговорить о реальных вещах и измерить время выполнения программ. Я реализовал четыре приведенных выше алгоритма на языке С на компьютере Pentium II 400 МГц, измерил скорость их работы и экстраполировал данные, сведя их в табл. 8.1. Время выполнения квадратичного алгоритма №2 обычно отличалось не более чем на 10% от квадратичного алгоритма №1, поэтому я не стал выделять его в отдельный столбец: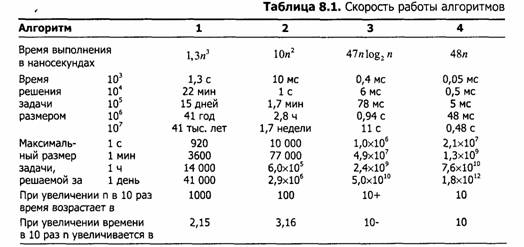
Эта таблица дает довольно много разнообразных сведений. Самый главный вывод: выбор правильного алгоритма может очень сильно влиять на время решения задачи. Это особенно подчеркивается в средней части таблицы. Последние две строки показывают, как связаны время решения задачи и ее размер.
Есть еще один важный момент. При сравнении кубического, квадратичного и линейного алгоритмов постоянные множители в выражениях для производительности значат не так уж много. Для быстрорастущих функций постоянные множители значат еще меньше. Чтобы подчеркнуть важность этого момента, я поставил эксперимент, в котором разница в постоянных множителях была максимально возможной. Алгоритм 4 был реализован на компьютере Radio Shack TRS-80 Model III (бытовой компьютер 1980 года выпуска с процессором Z80 на частоте 2.03 МГц). Чтобы еще больше замедлить его работу, я использовал интерпретатор Бейсика, что замедляет программу в 10-100 раз по сравнению с компилированным кодом. Алгоритм 1 был реализован на компьютере Alpha 21164 с частотой 533 МГц. Время выполнения кубического алгоритма росло по формуле 0,58n3 нc, а для линейного алгоритма - 19,5n мс (то есть 19 500 000n наносекунд или 50 элементов в секунду!). В таблице 8.2 показаны результаты экспериментов для различных размеров задачи:
Отношение постоянных множителей в виде 1/33 000 000 - давало некоторое преимущество кубическому алгоритму при малых размерах задачи, но линейный алгоритм неизбежно должен был нагнать кубический при увеличении n. Оба алгоритма решают задачу за одинаковое время при n ~ 5800; при этом обоим компьютерам требовалось около 2 мин: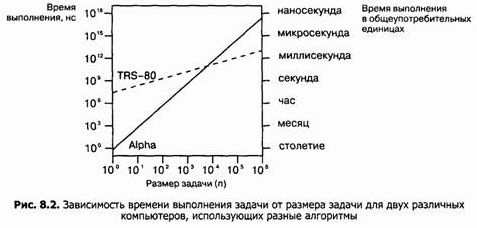
История
История задачи проливает свет на методы разработки алгоритмов. Наша небольшая задачка возникла в рамках работы по распознаванию образов, которой занимался Ульф Гренандер (Ulf Grenander) в Университете Брауна. Исходная задача была двумерной. При этом подмножество с максимальной суммой элементов отражало наибольшее соответствие между двумя цифровыми изображениями. Поскольку в двумерном варианте решить задачу было слишком тяжело, Гренандер упростил ее и занялся вначале одномерной, чтобы вникнуть в суть дела.
Гренандер решил, что кубический алгоритм выполняется слишком медленно, и придумал алгоритм 2. В 1977 году он рассказал о задаче Майклу Шамосу (Michael Shamos), который в тот же вечер придумал алгоритм 3. Когда Шамос вскоре после этого показал задачу мне, мы решили, что этот вариант алгоритма является лучшим из возможных, потому что незадолго до того исследователи показали, что несколько аналогичных задач могут быть решены только за время, пропорциональное ~ n*log n. Спустя несколько дней Шамос рассказал о задаче и ее истории на семинаре Карнеги Меллона (Carnegie Mellon), где присутствовал статистик Джей Кадан (Jay Kadane), который и набросал алгоритм 4, затратив на это приблизительно минуту. К счастью, мы знаем, что никакой алгоритм не может работать быстрее этого последнего четвертого варианта. Любой правильный алгоритм решения такой задачи потребует О(n) операций.
Хотя одномерная задача была решена полностью, исходная задача Гренандера в двумерной постановке остается открытой проблемой и сегодня, 20 лет спустя, когда второе издание этой книги выходит в печать. Из-за вычислительной трудоемкости всех известных алгоритмов Гренандеру пришлось отказаться(!!!) от этого подхода к распознаванию образов.
Эта история иллюстрирует ценные методы разработки алгоритмов.
Ценные методы, подходы
- Сохранение данных во избежание повторных вычислений
Эта простая форма динамического программирования использовалась в алгоритмах 2 и 4. Используя память для сохранения результатов, мы исключаем необходимость повторного их вычисления. - Предварительная обработка данных и помещение их в структуры
Структура cumarr в кубическом алгоритме №2 позволяет быстро вычислить сумму подпоследовательности. - Алгоритмы «разделяй и властвуй»
Алгоритм 3 использует правило «разделяй и властвуй». В учебниках по теории алгоритмов описаны более сложные формы применения этого правила. - Сканирующие алгоритмы
Задачи с массивами часто могут быть решены с помощью вопроса «как можно расширить решение задачи с х[0..i-1] до х[0..i]?». Алгоритм 4 сохраняет предыдущий результат и некоторые дополнительные данные для вычисления следующего результата. - Кумулятивные суммы
Алгоритм №2 использует таблицу кумулятивных сумм, где i-й элемент содержит кумулятивную сумму первых i значений массива х. Такие таблицы часто используются при работе с диапазонами. - Нижняя граница
Разработчики алгоритмов могут спокойно спать только тогда, когда они знают, что придуманный алгоритм — самый быстрый из возможных. Для этого им приходится доказывать существование нижней границы. Линейная скорость решения данной задачи была доказано. Доказательство существования нижних границ может быть достаточно сложным.
Реализации:
C++(1), C#(5) +добавить1) Еще один линейный алгоритм поиска максимальной суммы последовательности элементов в массиве на C++, code #629[аноним:Владимир]


