
Популярные задачи:
Простая быстрая сортировка
Коротко
Один из самых быстрых алгоритмов, позволяющих достигать производительности ~ O(n*log n). В исходной последовательности выбирается некоторый элемент. Затем пробегаемся по всей последовательности и элементы, меньшие чем выбранный располагаем слева от него, большие - справа. Затем эту же самую процедуру рекурсивно запускаем для 2-х полученных половинок. Т.е. в 2-х полученных последовательностях слева и справа от выбранного на первом шаге элемента - также выбираем некоторый опорный ключ и перебрасываем соответствующие большие и меньшие чем он элементы. Потом в уже 4-х полученных последовательностях - тоже самое. Пока не получим последовательности, состоящие лишь из одного элемента. После выполнения всех рекурсий в результате получаем отсортированную исходную последовательность.
При этом выбор этого опорного элемента на каждом шаге играет очень значительную роль, т.к. от этого зависит суммарная скорость выполнения всего алгоритма при различных условиях сортировки как-то: частичная упорядоченность элементов(один вариант выбора опорного элемента), наиболее хаотичное расположение элементов - другой вариант выбора и т.д. Самые распрастраненные здесь варианты - это выбор середины отрезка, выбор случайного элемента последовательности и выбор первого элемента последовательности. Последний вариант - является самым быстрым в общем случае и подробно расписывается ниже.
Подробно
По книге Джона Бентли:
"Жемчужины программирования"
"...Этот алгоритм был впервые описан К. А. Р. Хоаром в его классической статье «Быстрая сортировка» (С. A. R. Hoare, Quicksort. Computer Journal, 5, 1, April 1962, p. 10-15). В этом алгоритме используется подход «разделяй и властвуй», уже упоминавшийся в разделе 8.3: чтобы отсортировать массив, мы разделяем его на два подмассива и сортируем каждый из них рекурсивно. Например, для сортировки массива из восьми элементов:

мы разбиваем его первым элементом (55), так чтобы все элементы, меньшие 55, расположились слева от него, а все большие — справа.
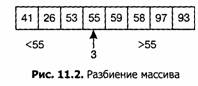
Если затем рекурсивно отсортировать подмножества х[0. .2] и х[4. .7] по отдельности, весь массив окажется отсортирован.
Среднее время работы этого алгоритма оказывается существенно меньшим 0(n2) сортировки вставкой, поскольку операция разбиения дает гораздо больше для достижения цели. После разбиения n элементов примерно половина из них окажется ниже выделенного элемента, а половина — выше. За то же самое время в программе сортировки вставкой на свое место устанавливается один-единственный элемент.
Итак, у нас есть набросок рекурсивной функции. Опишем рабочую часть массива с помощью индексов L, U (нижняя и верхняя границы). Рекурсия останавливается, когда мы добираемся до массива с числом элементов, меньшим двух. Т.о. получаем следующий набросок алгоритма:
Для разбиения массива относительно значения t мы начнем с простой схемы, о которой я узнал от Нико Ломуто. Более быстрый вариант этой программы, будет описан в следующем разделе(в задаче улучшение быстрой сортировки), но эта функция так проста, что в ней трудно ошибиться, и она ни в коем случае не может быть названа медленной. Пусть дано значение t, нужно упорядочить массив х[a..b] и вычислить индекс m такой, что все элементы, меньшие t, находятся слева от элемента х[m], а все большие — справа. Мы решим эту задачу с помощью простого цикла for, сканирующего массив слева направо, используя переменные i и m для сохранения инварианта:
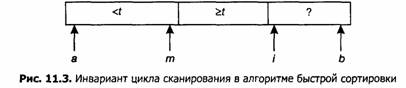
Когда проверяется i-й элемент, необходимо рассмотреть две ситуации. Если x[i] >= t, то инвариант остается истинным. Если же x[i] < t, то восстановить инвариант можно, увеличив индекс m (который указывает новое местоположение меньшего элемента) и поменяв местами x[i] и х[t]. В итоге получаем код, осуществляющий разбиение массива:
В алгоритме Quicksort нам нужно разбить массив x[L..U] относительно значения t=x[L], так что а = L + 1, и b = U. Инвариант цикла разбиения можно будет изобразить следующим образом:
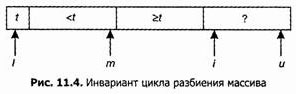
После завершения цикла получим следующую картину:
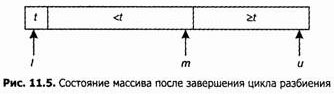
Затем мы поменяем местами x[t] и x[m], что даст следующее1:
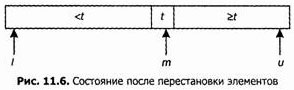
1Кажется соблазнительным пропустить этот этап и вызвать рекурсию с параметрами (L, t) и (t+1, U). К сожалению, при этом мы попадаем в бесконечный цикл, если t является наибольшим элементом массива. Возможно, я бы обнаружил эту ошибку в процессе проверки условия завершения, но читатель может догадаться, как я в действительности на нее наткнулся. М. Джейкоб дал элегантное доказательство некорректности такой программы: поскольку х[L] никогда не переставляется, эта сортировка будет работать только в том случае, если х[0] будет минимальным элементом массива.
Теперь можно рекурсивно вызвать функцию с параметрами (L, m-1) и (t+1, U).
Получившийся код дает первую завершенную версию быстрой сортировки. Для сортировки массива х[n] функцию следует вызвать как qsort (0, n-1):
В задаче 2 в конце главы(задача ускорение схемы Ломуто с помощью маркера) описана модификация алгоритма разбиения, предложенная Бобом Седжвиком (Bob Sedgewick). Она дает несколько более быстрый алгоритм qsort2.
Правильность этой программы была практически полностью доказана при ее выводе (как и должно быть). Доказательство ведется по индукции. Внешний оператор if правильно обрабатывает пустые и одноэлементные массивы, а алгоритм разбиения правильно подготавливает массивы большего размера для последующих рекурсивных вызовов. Программа не может войти в бесконечную последовательность рекурсивных вызовов, поскольку элемент х[m] при каждом таком вызове исключается. Таким же образом была доказана конечность алгоритма в задаче двоичного поиска.
Программа быстрой сортировки работает за время О(n*log n) и требует в среднем O(log n) памяти на стеке. Под «средним» случаем подразумевается случайная перестановка не равных друг другу элементов, поступающая на вход алгоритма. В большинстве учебников по теории алгоритмов подробно анализируется время выполнения быстрой сортировки. Кроме того, в них доказывается, что любая основанная на сравнении сортировка не может выполнить менее O(n*log n) сравнений, поэтому быстрая сортировка наиболее близка к идеалу.
Функция qsortl — это самая простая среди известных мне версия алгоритма быстрой сортировки. Она иллюстрирует важнейшие свойства этого алгоритма. Во-первых, он действительно быстр: в моей системе миллион случайных целых чисел упорядочивается чуть больше, чем за секунду, — вдвое быстрее, чем хорошо отлаженная библиотечная функция qsort языка С (последняя предназначена для сортировки различных типов данных, поэтому оказывается более медленной). Эта сортировка может быть удобной для некоторых приложений с хорошими входными данными, но она обладает и другим характерным свойством быстрых сортировок: для некоторых типов входных данных время ее работы может быть квадратичным. В следующем разделе(задача улучшение быстрой сортировки) рассмотрены более робастные быстрые сортировки.
..."
Джон Бентли
Реализации:
C++(2) +добавить1) Быстрая сортировка, опорный элемент - первый. на C++, code #14[автор:this]
2) Быстрая сортировка, выбор середины отрезка на C++, code #13[автор:-]


