Поразрядная сортировка массива подсчетом

• Формулировка
• Оптимизация
• Сравнительные диаграммы
• Все реализации

[Если вы еще не знакомы с поразрядной сортировкой как таковой, то быстрей прочитайте задачу поразрядная сортировка, общий принцип]

Формулировка

В классической поразрядной сортировке на каждом проходе, т.е. в пределах каждого разряда - элементы сортировались путем буквального разделения по каждому разряду, т.е. мы получали последовательности элементов, в каждой из которых содержались т.н. "одинаковые" элементы (идиентичны по конкретному текущему разряду). Очевидно, что для того, чтобы получить единую последовательность элементов отсортированных в пределах одного этого разряда - надо просто один за другой, по-порядку соединить все эти последовательности между собой.

Подход, о котором идет речь здесь - отличается тем, что на каждом проходе элементы исходной последовательности сортируются по конкретному текущему разряду не с помощью разделения по карманам, а с помощью подсчета элементов, которые меньше индекса некоторого дополнительного массива счетчиков. Т.е. никаких уже 2 этапов: распределения и сборки. Теперь можно сказать - только подсчет и вставка элементов в нужное место.

Подробнее. Те же основные итерации по каждому разряду максимально-разрядного числа, от младшего к старшему разряду. В пределах каждой итерации - составляем последовательность(назовем ее positions) из значений разрядов каждого элемента нашей последовательности, чтобы только с этими значениями на данной итерации и работать (сами числа нам не нужны конечно - только текущие их разряды). Далее составляем искомый массив счетчиков - count, размером range. Каждое его значение будет определять количество элементов из positions, которые меньше индекса данного элемента массива count. После того, как такой массив будет составлен - мы будем знать где на самом деле на данной итерации должен находится каждый элемент из positions, чтобы последний был отсортирован, поскольку для каждого элемента positions мы знаем количество элементов меньших чем он и поэтому встравляем его на соответствующее место.

Пример.
Пусть имеем исходную последовательность из 10-ти элементов source = {3, 1, 3, 9, 1, 4, 3, 2, 8, 3}.
Т.о. range = 10, width = 1, n = 10.
Составляем массив count размера range, т.е. в данном случае - 10. Пока инициируем его нулями. Далее проходимся по source от начала и до конца и для каждого его значения - просто увеличиваем(инкрементируем) соответствующий элемент count, что-то вроде:

for i = 0 to n-1
count[ source[i] ]++

Получаем: count = {0 2 1 4 1 0 0 0 1 1}

Далее проходимся по count и для каждого элемента считаем сумму предыдущих:

count[i] = count[0] + count[1] + ... + count[i-1]

В нашем случае получим: count = {0 0 2 3 7 8 8 8 8 9} Т.е. каждый count[i] - это количество элементов, меньших i. Это и является ключом метода. Теперь мы проходимся по всем source[i] и зная количество элементов меньших source[i]: count[ source[i] ](=K например) - просто вставляем source[i] на следующую позицию: K+1.

На этом, по-сути, сортировка для данного примера и заканчивается, т.е. имеем здесь только одну главную итерацию алгоритма, т.к. максимальное количество разрядов(width) = 1. Если бы в исходном массиве были бы двухзначные числа(56, 35), то имел бы место еще один проход, который бы отличался только тем, что на нем рассматривался бы еще и второй, более старший разряд элементов(ключей).

// Наш исходный сортируемый массив
x = {..<int> elements to be sorted...}
 
// Вспомогательная переменная
rangepow = 1
 
// Вспомогательный массив, 
// копирующий исходный X
source = array<int>[n] filled 0
 
for step = 0 to width-1
 
    // массив подсчета
    count = array<int>[range] filled 0
 
    // Копируем в source содержимое X
    // на текущей итерации
    source[] = copy of x[]
 
    // Получаем в count пока просто
    // количества текущих разрядов
    for i = 0 to n-1
        // d - это значение текущего разряда
        // для каждого нашего числа
        d = (source[i] / rangepow) % range
        count[ d ]++
 
    // Завершаем формирование count, т.е. получаем
    // количество элементов менших индекса
    summNum = 0  // вспомогательная переменная
    for i = 0 to range-1
        tmp       = count[i]
        count[i]  = summNum
        summNum  += tmp
 
 
    // Завершающий этап "вставка"
    for i = 0 to n-1
        d = (source[i] / rangepow) % range;
        x[ count[d] ] = source[i];  
        count[d]++; // Очень важная конструкция:
                    // для случая посторяющихся чисел.
    }
    rangepow *= range
 

Т.о. получаем, скорость ~ О(width*(2n + range)), память: ~(2n + range).

Оптимизация

Формирование ключевых массивов count можно начать заранее. Т.е. до запуска алгоритма, пробежавшись по нашему исходному массиву x - можно "наполовину" рассчитать все массивы count для каждого разряда, потому что неважно как расположены числа: количество одинаковых чисел по разрядам не меняется на каждом проходе. Поэтому если до основного цикла рассчитать все эти массивы count - на каждом проходе будет делаться лишь (n + range) операций, а не (2*n + range):

// Наш исходный сортируемый массив
x = {..<int> elements to be sorted...}
 
// Вспомогательный массив, 
// копирующий исходный X
source = array<int>[n] filled 0
 
// инициируем count пока нулями
// и кстати - теперь он двухмерный!
count = array<int>[width][n] filled 0
 
// рассчитываем количество чисел с 
// одинаковыми разрядами для всех значений
// разрядов
for i = 0 to n-1
    rangepow = 1
    for step = 0 to width-1
        d = (x[i] / rangepow) % range
        count[step][ d ]++;
 
// Вспомогательная переменная
rangepow = 1
 
for step = 0 to width-1
 
    // Копируем в source содержимое X
    // на текущей итерации
    source[] = copy of x[]
 
    // Завершаем формирование count, т.е. получаем
    // количество элементов менших индекса
    summNum = 0  // вспомогательная переменная
    for i = 0 to range-1
        tmp       = count[step][i]
        count[step][i]  = summNum
        summNum  += tmp
 
 
    // Завершающий этап "вставка"
    for i = 0 to n-1
        d = (source[i] / rangepow) % range
        x[ count[step][d] ] = source[i]
        count[step][d]++  // Очень важная конструкция:
                          // для случая посторяющихся чисел.
    }
    rangepow *= range
 

Т.о. получаем, сокращение скорости до: ~ O((width + 1)*(n + range)), но увеличение памяти до: ~(2n + width*range). Глядя на эту новую пропорцию скорости - выигрышь в производительности представляется не очень очевидным, но чисто логически рассуждая можно прийти к выводу, что общее количество проходов по исходному массиву x размера n - сокращается: с ~ 2*width*n, до (width + 1)*n.

Сравнительные диаграммы

Представляя на графиках производительности обеих алгоритмов(Graph1) и их отношение(т.е. насколько оптимизированная версия быстрее, Graph2) в зависимости от размера массива - n (при width=2, range=10), получим:

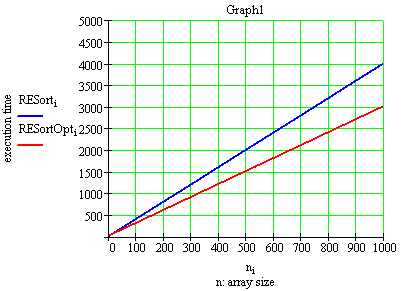
Как видим, наибольший выигрышь в скорости достигается на больших размерностях массива(>200). На малых же размерностях данная версия менее производительна(Graph3):

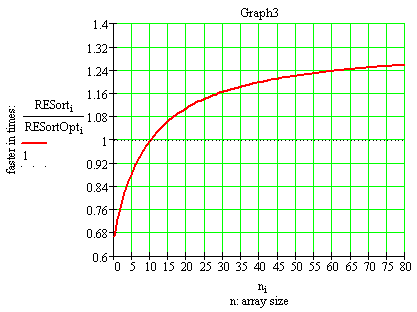
Точка перелома(n=10 в данном случае) очевидно определяется значениями width и range.

Что же касается увеличения расхода памяти, то при тех же условиях получим:

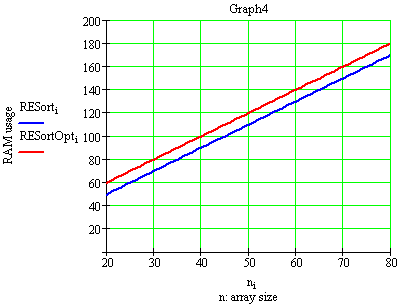
Т.е. на некоторую постоянную величину(определяющуюся значениями width и range) памяти будет расходоваться больше.

Реализации:

заполните необходимые поля!

название:
uri-имя*:
заголовок окна:
ЯП:	[другой...] pseudojavajavascriptpythonC++C#CphpGoqbasicrailsrubysmartytsqlvbnetvisualfoxproxmlactionscriptplsqlpascaloracle8sqlvbfortransmalltalkasmcssdelphigroovylispperlmysqlmatlab
код (double click - редактирование) (Esc - предпросмотр)
описание:
автор:	email:
пароль:	[для последующего редактирования]
	подписаться на комментарии**

*	можно кириллицей (недопустимые символы:?&+=\/%#)
**	только для зарегистрированных пользователей

 Поразрядная сортировка массива подсчетом, неоптимизированная версия ссылка |режим:

// глобальные константы (значения заданы для примера)
const int n = 10;
const int width = 2;
const int range = 10;
 
void RadixEnumSort(int x[]) {
    int source[n] = {0};
 
    for (int step = 0, rangepow = 1; step < width; step++, rangepow *= range) {
 
        int count[range] = {0};
        memcpy(source, x, sizeof(source));
 
        for (int i = 0; i < n; i++) {
            int d = (source[i] / rangepow) % range;
            count[ d ]++;
        }
 
        int summNum = 0;
        for (int i = 0; i < range; i++) {
            int tmp   = count[i];
            count[i]  = summNum;
            summNum  += tmp;
        }
 
        for (int i = 0; i < n; i++) {
            int d = (source[i] / rangepow) % range;
            x[ count[d] ] = source[i];
            count[d]++;
        }
    }
}

// глобальные константы (значения заданы для примера) const int n = 10; const int width = 2; const int range = 10; void RadixEnumSort(int x[]) { int source[n] = {0}; for (int step = 0, rangepow = 1; step < width; step++, rangepow *= range) { int count[range] = {0}; memcpy(source, x, sizeof(source)); for (int i = 0; i < n; i++) { int d = (source[i] / rangepow) % range; count[ d ]++; } int summNum = 0; for (int i = 0; i < range; i++) { int tmp = count[i]; count[i] = summNum; summNum += tmp; } for (int i = 0; i < n; i++) { int d = (source[i] / rangepow) % range; x[ count[d] ] = source[i]; count[d]++; } } }

Производительность: ~ О(width*(2n + range))
Расход памяти: ~ (2n + range)

Тестировалось на: MS Visual Studio 2005, .NET Framework 2.0

 

 Поразрядная сортировка массива подсчетом, оптимизированная версия ссылка |режим:

// глобальные константы (значения заданы для примера)
const int n = 10;
const int width = 2;
const int range = 10;
 
void RadixEnumSortOpt(int x[]) {
 
    int source[n] = {0};    
    int count[width][range] = {0};
 
    for (int i = 0; i < n; i++) {
        for (int step = 0, rangepow = 1; step < width; step++, rangepow *= range) {
            int d = (x[i] / rangepow) % range;
            count[step][ d ]++;
        }
    }
 
    for (int step = 0, rangepow = 1; step < width; step++, rangepow *= range) {
        memcpy(source, x, sizeof(source));
 
        int summNum = 0;
        for (int i = 0; i < range; i++) {
            int tmp = count[step][i];
            count[step][i] = summNum;
            summNum += tmp;
        }
 
        for (int i = 0; i < n; i++) {
            int c = (source[i] / rangepow) % range;
            x[ count[step][c] ] = source[i];
            count[step][c]++;
        }
    }
}

// глобальные константы (значения заданы для примера) const int n = 10; const int width = 2; const int range = 10; void RadixEnumSortOpt(int x[]) { int source[n] = {0}; int count[width][range] = {0}; for (int i = 0; i < n; i++) { for (int step = 0, rangepow = 1; step < width; step++, rangepow *= range) { int d = (x[i] / rangepow) % range; count[step][ d ]++; } } for (int step = 0, rangepow = 1; step < width; step++, rangepow *= range) { memcpy(source, x, sizeof(source)); int summNum = 0; for (int i = 0; i < range; i++) { int tmp = count[step][i]; count[step][i] = summNum; summNum += tmp; } for (int i = 0; i < n; i++) { int c = (source[i] / rangepow) % range; x[ count[step][c] ] = source[i]; count[step][c]++; } } }

Производительность: ~ O((width + 1)*(n + range))
Расход памяти: ~ (2n + width*range)

Тестировалось на: MS Visual Studio 2005, .NET Framework 2.0