
Популярные задачи:
Улучшение быстрой сортировки
Коротко:
Быстрая сортировка(функция qsort1) достаточно хорошо справляется с массивом случайных чисел, но если на вход подается уже частично упорядоченная последовательность либо последовательность содержащая подпоследовательности из одинаковых элементов, расположенных рядом - время выполнения алгоритма значительно возрастает, стремясь к ~ O(n2). В тоже время такой алгоритм как сортировка вставкой - с такими случаями справляется "на ура", сортируя со скоростью ~ O(n). Поэтому используем здесь следующий подход: если в сортируемой последовательности в алгоритме быстрой сортировке остается меньше cutoff элементов - они сортируется сортировкой вставками. cutoff - некоторая константа(которая зависит от начальных условий и обычно равна 3-40).
Подробно:
По книге Джона Бентли:
"Жемчужины программирования"
"...Функция qsort1 быстро сортирует массив случайных чисел, но что, если на вход будет подана уже упорядоченная последовательность? Программисты часто используют сортировку для того, чтобы одинаковые элементы оказались рядом. Следовательно, нужно рассмотреть крайний случай: массив из n одинаковых элементов. Сортировка вставкой работает на таких данных очень быстро: каждый элемент сдвигается на 0 позиций, поэтому время выполнения растет как О(n). Функция qsort1 справляется с такими данными очень плохо. Каждое из n-1 разбиений требует время О(n) для выделения одного элемента, поэтому полное время выполнения растет как О(n2). Время обработки для n = 1 000 000 возрастает с одной секунды до двух часов.
Можно обойти эту проблему, используя двусторонний алгоритм разбиения с приведенным на рис. 11.7 инвариантом:
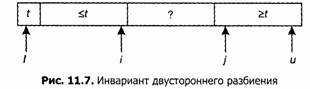
Индексы i и j инициализируются граничными индексами разбиваемого массива. Главный цикл содержит два вложенных цикла. Первый вложенный цикл сдвигает i вверх, пропуская меньшие элементы, а второй увеличивает j, пропуская большие элементы и останавливаясь на меньшем. Главный цикл проверяет, не пересекаются ли эти индексы, и переставляет соответствующие элементы.
Но как такой код будет работать в ситуации, когда все элементы равны? Первая мысль: пропустить эти элементы, чтобы не делать лишней работы, но в результате получается квадратичный для массива из одинаковых элементов алгоритм. Поэтому каждое сканирование будет останавливаться на одинаковых элементах, которые затем будут обмениваться. Хотя в этом варианте обменов будет производиться больше, чем требуется, такая программа будет превращать худший случай с массивом из одинаковых элементов в лучший, требующий почти в точности n*log2n и сравнений. Псевдокод, реализующий описанный алгоритм разбиения, примет вид:
Избавляясь от квадратичного поведения в худшем случае, этот код и в среднем делает меньше обменов, чем qsort1.
Рассмотренные нами программы быстрой сортировки разбивали массив относительно первого встреченного элемента. Это хорошо подходит для случайных входных данных, но может сильно замедлить работу для некоторых упорядоченных последовательностей. Если массив уже отсортирован по возрастанию, его придется разбивать относительно первого элемента, затем относительно второго и так далее, что потребует времени О(n2). Мы можем избежать этого, выбирая элемент для разбиения случайным образом — обменивая местами элемент х[l] со случайным элементом из диапазона x[l..u]:
swap(l, randint(l, u))
Если у вас нет функции randint, обратитесь к задаче, которая посвящена написанию собственного генератора случайных чисел(прим. ред.:на данном сайте этому посвящана задача собственный генератор случайных чисел). Каким бы кодом вы ни пользовались, внимательно проследите за тем, чтобы функция randint возвращала значение из диапазона [l, u] — выход за его границы приведет к ошибкам. Объединив случайный выбор центрального элемента с двусторонним разбиением, мы получим программу быстрой сортировки, работающую за время O(n*log n) для любого входного массива. Усреднение делается вызовом генератора случайных чисел, а не анализом возможного распределения входных данных.
Наша программа быстрой сортировки большую часть времени тратит на сортировку очень маленьких подмножеств. Такие массивы было бы проще всего сортировать каким-либо несложным методом вроде сортировки вставкой, а не тратить на них всю мощь быстрой сортировки. Боб Седжвик разработал весьма хитроумную реализацию этой идеи. Когда функция быстрой сортировки вызывается для небольшого массива (то есть l и u близки), она не делает ничего. Реализуется это путем замены первого оператора if нашей функции на следующий код:
if u-l > cutoff return
Здесь cutoff — некоторое небольшое целое число. После завершения работы функции массив будет не отсортирован до конца, но разбит на небольшие группы случайно упорядоченных элементов, причем все элементы одной группы будут меньше любого элемента всех групп, расположенных справа от данной. Сортировать элементы внутри групп нужно каким-то другим методом, и тут лучше всего подходит сортировка вставкой, поскольку массив уже почти упорядочен.
Для решения задачи сортировки целиком придется выполнить два вызова:
qsort4(0, n-1)
isort3()
На последнем этапе оптимизации программы можно раскрыть вызов функции swap во внутреннем цикле (поскольку другие два вызова swap лежат вне внутреннего цикла, их раскрытие не даст ощутимого результата). Последняя версия программы Quicksort примет вид:
В табл. 11.2 приведены сводные данные по всем версиям быстрой сортировки. Правая колонка указывает среднее время работы в наносекундах, требуемое для сортировки массива из n случайных целых чисел. Многие алгоритмы могут вести себя как квадратичные для некоторых конкретных входных данных.

Функция qsort состоит из 15 строк быстрой сортировки и 5 строк сортировки вставкой. Для миллиона случайных чисел время выполнения лежит в диапазоне от 0,6 с для библиотечной функции sort языка C++ до 2,7 с для библиотечной функции qsort языка С.
..."
Джон Бентли
Реализации:
C++(2) +добавить1) Быстрая сортировка QSort3 (оптимизация №1) на C++, code #15[автор:this]
2) Быстрая сортировка QSort4 (оптимизация №2) на C++, code #16[автор:this]


