
Популярные задачи:
Бинарный поиск в массиве и его разновидности
Коротко
Выполняется на упорядоченном одномерном массиве. Производит самый быстрый поиск при таких условиях.
Максимальное количество сравнений(проходов) log2n. Работает следующим образом: смотрим середину первоначального интервала - больше, меньше, равна ли искомому значению? Если равна - понятно что делаем, если меньше, то делаем новый интервал, который начинается с середины предыдущего интервала и заканчивается той же верхней границей предыдущего, т.е. это как-бы вторая половина исходного интервала, далее вся процедура повторяется. Если середина - больше искомого значения, то новый интервал будет первой половиной исходного интервала. И так итеративно сужаем наш интервал до тех пор, пока искомый элемент не будет найден или не дойдем до пустого интервала.
Соответственно: x[] - массив, где ищем; l и u - динамически изменяемые границы сужаемого интервала, то что им присваются вначале значения -1 и n, то это инициализируются фиктивные значения, которые никогда не будут использованы программой, но которые позволяют избежать лишних if-ов в коде, получая в конечном итоге более оптимизированный код. p - это индекс искомого элемента, если элемент не найден, то в конечном счете он будет = -1. Если искомых елементов в массиве несколько - будет возвращен индекс первого из них.
Подробно
Наиболее полно простоту и мощь двоичного(бинарного) поиска описал Джон Бентли в своей книге "Жемчужины программирования":
"...Я задумываю целое число от 1 до 100, а вы его угадываете. 50? Мало. 75? Много. И так игра продолжается до тех пор, пока вы не угадаете задуманное мною число. Если число взято из диапазона 1..n, то оно может быть наверняка угадано за log2n попыток. Если n=1000, достаточно будет 10 попыток, а если n=1 000 000, потребуется не более 20 попыток.
Этот пример иллюстрирует метод, позволяющий решить множество задач программирования, — двоичный поиск. В начальный момент мы знаем, что объект находится в заданной области, а операция выбора и проверки значения сообщает нам, где находится объект: в текущей позиции, выше или ниже ее. При двоичном поиске местоположение объекта обнаруживается с помощью повторяющегося выбора элемента из середины текущей области. Если выбранный элемент отличается от искомого, текущая область делится пополам, после чего процесс выбора и сравнения повторяется. Поиск закончен, если обнаруживается искомый элемент или пустая область.
Самое обычное применение двоичного поиска — поиск элемента в отсортированном массиве. При поиске числа 50 будут проверены следующие элементы (рис. 2.1).
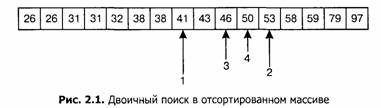
Программа последовательного поиска выполняет в среднем около n/2 сравнений при поиске в наборе из n элементов, тогда как двоичный поиск всегда делает не более log2n. Этот факт может очень сильно повлиять на производительность системы. Вот пример, относящийся к системе бронирования билетов авиакомпании TWA:
«Одна из программ осуществляла последовательный поиск в огромном объеме памяти примерно 100 раз в секунду. По мере роста сети среднее время обработки сообщения возросло до 0,3 мс, что оказалось для нас слишком много. Мы установили, что проблема заключается в использовании процедуры последовательного поиска, заменили ее процедурой двоичного поиска, и проблема исчезла».
Я часто сталкивался с этим и в других системах. Программисты начинают с простой структуры данных и последовательного поиска, который поначалу оказывается достаточно быстрым. Когда производительности подобной программы начинает не хватать, можно отсортировать таблицу и воспользоваться двоичным поиском, что устраняет проблему.
Однако поле применения двоичного поиска не ограничивается быстрым поиском в отсортированных массивах. Рой Вейл (Roy Weil) применил этот метод для нахождения некорректной строки во входном файле, содержащем более 1000 строк. К сожалению, строку эту нельзя было обнаружить по ее внешнему виду; узнать о ее наличии можно было, лишь обработав файл (начальную часть до произвольного места) некой программой и получив некорректный ответ, на что требовалось несколько минут. Его предшественники, пытавшиеся найти ошибку, пробовали обрабатывать несколько строк за один проход, благодаря чему продвигались к цели со скоростью улитки. Попробуйте догадаться, как удалось Вейлу найти ошибку за десять попыток?..."
Пишем программу
"...Алгоритм двоичного поиска решает задачу, уменьшая размер поддиапазона, в котором может находиться t (если это число вообще есть в массиве). В начале диапазоном является весь массив. Затем его средний элемент сравнивается с t, после чего половина диапазона исключается из рассмотрения. Процесс продолжается до тех пор, пока число t не будет найдено или пока диапазон, в котором оно должно находиться, не окажется пуст. Для массива из n элементов двоичный поиск выполняет около Lg N сравнений.
Большинство программистов полагают, что по подобному описанию написать программу не составляет труда. Они ошибаются. Единственный способ заставить вас поверить в это: отложите книгу и попробуйте сами написать программу. Попробуйте!
Я предлагал проделать подобную работу слушателям курсов для профессиональных программистов. Им давалось несколько часов на то, чтобы сделать программу по данному им описанию на произвольном, выбранном ими языке, кроме того, разрешалось воспользоваться псевдокодом высокого уровня. К концу предложенного времени почти все отвечали, что они готовы. На проверку их кода с помощью тестов отводилось еще тридцать минут. Статистика по нескольким классам, в которых обучалось более ста человек, получилась такая: 90% программистов нашли ошибки в своих программах (и я не всегда был уверен в правильности текстов тех, у кого явных ошибок обнаружено не было).
Я был удивлен. Имея в запасе практически неограниченное время, только 10% профессиональных программистов смогли написать эту небольшую программу правильно. Эта задача оказалась не по зубам не только моим ученикам: раздел 6.2.1 третьего тома книги Кнута «Искусство программирования для ЭВМ: сортировка и поиск» посвящен истории этого алгоритма, и в нем Кнут отмечает, что, хотя первая программа двоичного поиска была опубликована в 1946 году, программа, не содержащая ошибок, появилась лишь в 1962 году.
Основная идея двоичного поиска состоит в том, что мы всегда знаем, что если t вообще есть в массиве, то оно должно быть в выбранном нами поддиапазоне. Мы будем использовать выражение mustbe (range) для отражения того факта, что если t есть в массиве, то оно есть и в исследуемом на данном этапе диапазоне range. Мы воспользуемся этой записью, чтобы превратить описание двоичного поиска в набросок программы(Листинг 4.1):
Важной частью этой программы является инвариант цикла (loop invariant), заключенный в фигурные скобки. Это утверждение, относящееся к состоянию программы, называется инвариантом, поскольку оно остается истинным в начале и в конце каждой из итераций; это формализация того интуитивного утверждения, которое мы сделали выше.
Теперь займемся усовершенствованием нашей программы, заботясь о сохранности инварианта в ходе всех наших действий. Прежде всего, нам нужно как-то представить диапазон. Для этого мы будем использовать два индекса l и u, задающие нижнюю и верхнюю границы диапазона L,U. Логическая функция mustbe(l, u) утверждает, что если число t вообще есть в массиве, то оно обязательно принадлежит диапазону х[l,u], включая границы диапазона.
Затем нужно заняться инициализацией. Какими должны быть значения l и u, чтобы утверждение mustbe(l, u) было истинным? Очевидный выбор: 0 и n-1: утверждение mustbe(0, n-1) сводится к тому, что если t есть в массиве х, то оно принадлежит х[0, n-1], а именно это и известно нам с самого начала. Следовательно, инициализация будет состоять в присваивании значений l=0 и u=n-l.
Затем нужно проверить диапазон на наличие в нем вообще каких-либо элементов, после чего найти его середину m. Диапазон l...u является пустым, если l > u, и в этом случае мы помещаем в переменную р специальное значение -1, завершая цикл. Переменная p - это результат, т.е. позиция(индекс) искомого элемента в массиве. Для нахождения середины m используем целочисленное деление: m = (l + u) / 2;
Итак, наша усовершенствованная программа выглядит теперь следующим образом (листинг 4.2):
Теперь нужно в явном виде записать последние три строки. Для этого необходимо сравнить t и х[m], после чего выполнить определенное действие для сохранения инварианта. Действие это будет выполняться по следующей схеме:
case
x[m] < t action a
x[m] == t action b
x[m] > t action с
Действие b, очевидно, будет состоять в присваивании р=m и выходе из цикла, поскольку выполнение условия означает, что мы нашли элемент, равный t Оставшиеся два случая симметричны, мы займемся первым, а второй получим из него по соображениям симметрии (это одна из причин, по которым мы будем очень аккуратны при проверке кода в следующем разделе).
Если x[m] < t, мы понимаем, что х[0] <= х[1] <= ..<= x[m] < t, поэтому t не может принадлежать диапазону х[0..m]. Поскольку мы знаем также, что t не может не принадлежать x[l..u], мы понимаем, что если t где-нибудь есть, то оно принадлежит диапазону x[m + 1,u], что мы запишем в форме mustbe(m+1, u). Поэтому мы восстановим инвариант mustbe(l, u) путем присваивания l = m+1. Уточнив, таким образом, предыдущий набросок, получим листинг 4.3.
Программа получилась короткой: десяток строк кода и один инвариант. Простейший способ проверки программы — запись инварианта и сохранение его неизменным в процессе написания программы — оказался очень полезным при переписывании наброска алгоритма на псевдокоде. Этот процесс дал нам некоторую уверенность в программе, но мы ни в коем случае не можем считать ее правильной. Прежде чем читать дальше, потратьте несколько минут, чтобы проверить, правильно ли она работает..."
На С++ данный код будет выглядеть таким образом.
Оптимизируем двоичный поиск
"...Обратимся к одному из наиболее ярких примеров оптимизации программ. Обычно оптимизировать двоичный поиск не требуется — алгоритм и так достаточно эффективен. Именно поэтому мы игнорировали возможность микроскопического повышения эффективности ранее, когда нашей задачей стояло получение простой и верной программы, которую было бы легко сопровождать. Однако иногда оптимизация поиска оказывает существенное влияние на производительность большой системы в целом.
Разрабатывать быструю версию двоичного поиска мы будем постепенно, в четыре этапа. Промежуточные программы достаточно сложны, но существует веская причина изучить их внимательно: последняя версия программы работает в 2-3 раза быстрее, чем исходная. Прежде чем вы продолжите чтение, попробуйте найти в базовой реализации явные «излишки», от которых можно избавиться.
Мы начнем работу над оптимизацией двоичного поиска с изменения условия задачи. Пусть требуется найти первое вхождение t в массиве х[0..n-1] (приведенная базовая реализация возвращает произвольное вхождение). Основной цикл программы будет выглядеть так же. Мы сохраним индексы l и u, ограничивающие область поиска элемента t, но инвариант будет другим: x[l] < t <= x[u] и l < u. Мы предположим, что n >= 0, х[-1] < t и x[n] >= t, где x[-1] и x[n] - фиктивные, искусственные (но программа никогда не будет обращаться к ним, к этим фиктивным элементам). Новая версия двоичного поиска будет выглядеть как:
B первой строке мы инициализируем инвариант. При повторных проходах тела цикла инвариант сохраняется при помощи оператора if: легко доказать, что обе ветви сохраняют инвариант. При завершении работы мы можем быть уверены, что если t есть в массиве, то его позиция возвращается в переменной u. Этот факт более формально выражен в утверждении. Последние две строки присваивают р индекс первого вхождения t в массив х или -1 в случае отсутствия t в массиве.
Хотя эта программа решает более сложную задачу, чем предыдущая, она потенциально более эффективна, поскольку на каждой итерации выполняется только одно сравнение t с элементом массива х. Предыдущей программе в некоторых случаях приходилось производить две такие проверки.
Следующая версия программы будет использовать известный нам факт, заключающийся в том, что n = 1000. Мы представим диапазон по-другому, используя нижнюю границу l и добавку i вместо нижней и верхней границ (l и u). Код будет гарантировать, что i всегда равно какой-либо степени двойки. Это свойство легко сохранить после того, как оно впервые окажется верным, но сделать его верным достаточно сложно (поскольку размер массива — 1000). Поэтому перед основным циклом программы нужно поставить условный оператор и оператор присваивания, которые сузят начальный диапазон до 512 (наибольшая степень двойки, меньшая 1000). Значения l и l+i позволяют задать диапазон -1..511 или 488..1000. Переделав программу, получим листинг 4.5.
Доказательство правильности этой программы проводится так же, как и для предыдущей. Этот вариант обычно работает медленнее предшествующего, но он дает возможность дальнейшего повышения производительности.
Следующая программа является упрощением данной. Она учитывает возможность автоматической оптимизации, обеспечиваемой при компиляции. Упрощается первый оператор if, убирается переменная nexti, и присваивания, где она участвовала, удаляются из внутреннего оператора if.
Хотя корректность алгоритма доказывается тем же путем, что и раньше, мы уже лучше понимаем его работу на интуитивном уровне. Когда первая проверка оказывается неправильной и переменная l остается нулевой, программа находит биты р в порядке убывания значимости.
Последняя версия программы написана не от отчаяния. Она удаляет издержки на структуру цикла и деление i/2 путем раскрытия цикла в явном виде. Поскольку i принимает десять конкретных значений, мы можем закодировать их в нашей программе. Тогда нам не придется их вычислять во время ее выполнения:
Утверждения позволяют лучше понять работу программы. Проведя анализ одного оператора if и поняв, что происходит в обоих случаях, вы легко разберетесь и со всем остальным.
Я сравнивал «простой» двоичный поиск с этой оптимизированной версией в разных системах. В первом издании этой книги приводилось время работы программ с различными уровнями оптимизации на четырех компьютерах и пяти языках программирования. Коэффициент ускорения менялся от 1,38 до 5 (что соответствует сокращению времени работы на 80%). Когда я измерил скорость работы исходной и оптимизированной программ на моем нынешнем компьютере, я с удивлением обнаружил, что время работы для n = 1000 сократилось с 350 до 125 не (сокращение времени работы на 64%).
Результат показался мне слишком хорошим, и вскоре обнаружилось, что он действительно не был вполне корректным. Тестовая программа осуществляла последовательный поиск элементов (сначала х[0], затем х[1] и так далее), что давало подпрограмме двоичного поиска преимущество, поскольку допускало предсказание ветвления алгоритма. Изменив тестовую программу так, чтобы поиск элементов производился случайным образом, я получил новый результат: 418 не для основной версии и 266 нc — для оптимизированной (36% сокращение времени).
Итого
Мы разобрали предельный случай оптимизации. Очевидная версия программы двоичного поиска (которая казалась достаточно стройной) была заменена оптимизированной, в которой нет уж совсем ничего лишнего. (Эта функция была написана впервые в начале 60-х. Я услышал о ней от Гая Стила (Guy Steele) в начале 80-х, а он изучал ее в MIT. Вик Высоцкий использовал этот код в Bell Labs в 1961 году. Каждый оператор if псевдокода можно было реализовать тремя командами IBM 7090.)..."
Джон Бентли
Реализации:
java(1), C++(3), C#(2), php(2) +добавить1) Алгоритм бинарного поиска на java, code #795[автор:this]


